原文链接：python模块：Scipy.optimize.linprog线性规划求解

一、模块介绍

1.1模块功能

Scipy.optimize是Scipy中一个用于解决数学模型中优化类模型的子包，该子包中又包含了多个子功能模块见下表，不同方法不同条件求解最优化模型。本节介绍linprog对线性规划问题的模型建立与求解。

问题类型	模块
多元标量函数的有/无约束最小化	minimize
最小二乘法最小化	least_squares
单变量函数最小化器	minimize_scalar
线性规划	linprog

1.2模型介绍

线性规划模型是指一种特殊形式的数学规划模型，即目标函数和约束条件是待求变量的线性函数、线性等式或线性不等式的数学规划模型。根据问题背景，经过对问题的分析，通过三个步骤建立数学模型：1.确定决策变量，2.建立目标函数，3.指定约束条件。

由于目标函数和约束条件都是由决策变量组成的线性函数表达式，由此可以表示为下图所示形式。

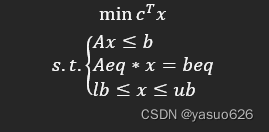
x为决策变量形成的列向量，c是决策变量的系数列向量。首行给出目标函数，$min \quad f(x)$ 或$max \quad f(x)$，为了与linprog格式一致，$max f(x)$我们转换为$min \quad -f(x)$ 。s.t.括号中的则表示约束条件。我们将约束分为等式和不等式的约束，以及对于决策变量的约束。

由于线性规划模型约束为线性函数，每个约束式都是决策变量一次式，每个约束式决策变量的系数可以表示为向量形式，假设不等式约束有m1个，决策向量维度为n，则可将所有不等式约束可综合表示为系数矩阵A与决策向量乘积形式，b则是约束阈值的列向量。

对于约束中≥阈值的约束可以与目标函数一样取负值转换。同样可以得到等式约束的矩阵形式和决策变量定义域范围上下限向量表示。

二、模块源分析与参数解释

2.1 linprog模块分析

def linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None,
            bounds=None, method='interior-point', callback=None,
            options=None, x0=None)

参数对应的意义可由表2.1详细表示，对应于1.2中建立的线性规划模型，linprog可以看出是一个很直观简单的方法（对于矩阵和向量用numpy数组表示）

参数	意义
c	目标函数的决策变量对应的系数向量(行列向量都可以，下同)
A_ub	不等式约束组成的决策变量系数矩阵
b_ub	由A_ub对应不等式顺序的阈值向量
A_eq	等式约束组成的决策变量系数矩阵
b_eq	由A_ub对应等式顺序的阈值向量
bounds	表示决策变量x连续的定义域的n×2维矩阵，None表示无穷
method	调用的求解方法，2.2节给出详细解释
callback	选择的回调函数
options	求解器选择的字典
x0	初始假设的决策变量向量，若可行linprog会对方法优化

2.2参数解释

对于method参数是选择linprog的求解器方法，可选参数由一个字典包括

1	LINPROG_METHODS = ['simplex', 'revised simplex', 'interior-point', 'highs', 'highs-ds', 'highs-ipm']

在 osgeo.cn 的scipy文档中对method的方法给出以下解释：

方法 ‘highs-ds’ 是C++高性能双重修订单工实现(HSOL)的包装器 [13], [14]. 方法 ‘highs-ipm’ 是C++实现的 i n前面-p oint m 方法 [13]; 它的特点是交叉例程，因此它与单纯形求解器一样精确。方法 ‘highs’ 自动在两者之间进行选择。有关涉及以下内容的新代码 linprog ，我们建议显式选择这三个方法值中的一个，而不是 ‘interior-point’ (默认)， ‘revised simplex’ ，以及 ‘simplex’ (旧版)。

即建议用户选择highs的三个方法，这在速度和精度上都更加优越，选择highs方法自动选择两个方法中的较好的一个。而在实例中我们会得到method为highs和默认的interior-point方法的区别。

三、实例求解

3.1求解实例

我们给出一个简单的线性规划模型实例:

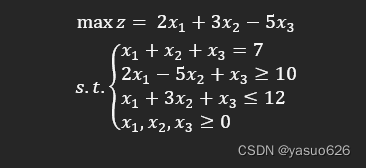
按照模型得到决策变量，目标函数，两个不等式约束，一个等式约束，以及给出定义域。将对应linprog参数由numpy处理过后的数据赋值传入参数即可求解出最优值与对应的决策变量取值。

注意：

（1）linprog目标函数此时为最大化，要按上述方法转为最小化。

（2）同时对于仅有一个约束的矩阵不能直接传入一维的数组，而应该表示为一个只有一个向量的二维矩阵形式。

3.2求解代码

python的求解代码给出为：

"""
数学规划模型
scppy.optimize.linprog
"""
from scipy.optimize import linprog
import numpy as np
c=np.array([-2,-3,5]).transpose()    #行列向量不影响求解
A=np.array([[-2,5,-1],[1,3,1]])
b=np.array([-10,12])
Aeq=np.array([[1,1,1]])    # 单个约束也要表示为矩阵形式
beq=np.array([7])
x=linprog(c,A,b,Aeq,beq,method='highs',bounds=np.array([[0,None],[0,None],[0,None]]))
print(x)

3.3结果分析与比较

我们得到上述method=’highs’求解的结果：

con: array([0.])
crossover_nit: 0
eqlin: marginals: array([-2.28571429])
residual: array([0.])
fun: -14.571428571428573
ineqlin: marginals: array([-0.14285714, -0. ])
residual: array([0. , 3.85714286])
lower: marginals: array([0. , 0. , 7.14285714])
residual: array([6.42857143, 0.57142857, 0. ])
message: ‘Optimization terminated successfully.’
nit: 3
slack: array([0. , 3.85714286])
status: 0
success: True
upper: marginals: array([0., 0., 0.])
residual: array([inf, inf, inf])
x: array([6.42857143, 0.57142857, 0. ])

与默认方法结果比较：

con: array([1.80714554e-09])
fun: -14.571428565645032
message: ‘Optimization terminated successfully.’
nit: 5
slack: array([-2.24602559e-10, 3.85714286e+00])
status: 0
success: True
x: array([6.42857143e+00, 5.71428571e-01, 2.35900788e-10])

message给出模型求解成功提示，nit为迭代数，决策变量以x的数组形式返回，最优值为fun。

两个方法都能正确求解出结果，highs方法迭代次数更少，并且给出了边际和残余值。比较得出highs比默认方法更加高效，建议使用highs方法求解。